Modeling and design of many types of equipment for separating gas and liquids such as flash separators at the well head, distillation columns and even a pipeline are based on the phases present being in vapor-liquid equilibrium. The thermodynamic equilibrium between vapor and liquid phases is expressed in terms equality of fugacity of component i in the vapor phase, fiV, and the fugacity of component i in the liquid phase, fiL, is written as
Equation (1) is the foundation of vapor-liquid equilibrium calculations; however, we rarely use it in this form for practical applications. For calculation purposes, Eq. (1) is transformed to a more common expression which is
Ki is called the vapor–liquid equilibrium ratio, or simply the K-value, and represents the ratio of the mole fraction in the vapor, yi, to the mole fraction in the liquid, xi. Equation (2) is also called “Henry’s law” and K is referred to as Henry’s constant. For the more volatile components the Kvalues are greater than 1.0, whereas for the less volatile components they are less than 1.0.
Depending on the system under study, any one of several approaches may be used to determine K-values. Obviously, experimental measurement is the most desirable; however, it is expensive and time consuming. Alternatively, there are several graphical or numerical tools that are used for determination of K-values. This “Tip of the Month” presents a history of many of those graphical methods and numerical techniques.
In general K-values are function of the pressure, temperature, and composition of the vapor and liquid phases. The components making up the system plus temperature, pressure, composition, and degree of polarity affect the accuracy and applicability, and hence the selection, of an approach. The widely used approaches are K-value charts, Raoult’s law, the equation of state (EoS) approach (f), activity coefficient approach (?) or combination of EoS and the EoS and ? approaches [1-5]. EoS approach requires use of a digital computer.
K-Value Charts
There are several forms of K-value charts. One of the earliest K-value charts for light hydrocarbons is presented in reference [1]. In these charts, K-values for individual components are plotted as a function of temperature on the x-axis with pressure as a parameter. In each chart the pressure range is from 70 to 7000 kPa (10 to 1000 psia) and the temperature range is from 5 to 260 ºC (40 to 500 ºF).
Early high pressure experimental work revealed that, if a hydrocarbon system of fixed overall composition were held at constant temperature and the pressure varied, the K-values of all components converged toward a common value of unity (1.0) at some high pressure. This pressure was termed the “Convergence Pressure” of the system and has been used to correlate the effect of composition on K-values, thus permitting generalized K-values to be presented in a moderate number of charts.
In more recent publications [2], the K-values are plotted as a function of pressure on the x-axis with temperature and Convergence Pressure as parameters. In order to use these charts, one should determine the Convergence Pressure first. The determination of convergence Pressure is a trial-and-error procedure and can be found elsewhere [6].
For computer use, later in 1958 these K-Value charts were curve fitted to the following equations by academic and industrial experts collaborating through the Natural Gas Association of America [7].
In Eq (3) T is temperature in ºR, P is pressure in psia and the fitted values of the bij coefficients are reported in an NGAA publication [7].
A relatively simple nomograph is normally presented in undergraduate thermodynamics and unit operations text books. In the nomograph, the K-values of light hydrocarbons, normally methane through n-decane, are plotted on one or two pages. Charts of this type do allow for an average effect of composition, but the essential basis is Raoult’s law and equilibrium constants derived from them are useful only for teaching and academic purposes.
Raoult’s Law
Raoult’s Law is based on the assumptions that the vapor phase behaves as an ideal gas and the liquid phase is an ideal solution. Under these conditions the fugacities are expressed as
The saturation pressure of a component is represented by PiSat and the pressure of the system is represented by P. Substituting from Eqs (4) and (5) in Eq (1) gives
The vapor pressure may be read from a Cox chart or calculated from a suitable equation in terms of temperature. A typical Cox chart may be found in reference [8]. The Antoine [5] equation is recommended for calculating vapor pressure:
Values of A, B, and C for several compounds are reported in the literature [5]. Complex vapor pressure equations such as presented by Wagner [5], even though more accurate, should be avoided because they can not be used to extrapolate to temperatures beyond the critical temperature of each component. Raoult’s law is applicable to low pressure systems (up to about 50 psia or 0.35 MPa) or to systems whose components are very similar such as benzene and toluene. This method is simple but it suffers when the temperature of the system is above the critical temperature of one or more of the components in the mixture. At temperatures above the critical point of a component, one must extrapolate the vapor pressure which frequently results in erroneous K-values. In addition, this method ignores the fact that the K-values are composition dependent.
Correlation Method
As mentioned earlier, determination of K-values from charts is inconvenient for computer calculations. Therefore, scientists and engineers have developed numerous curve fitted expressions for calculation of K-values. However, these correlations have limited application because they are specific to a certain system or applicable over a limited range of conditions. Some of these are polynomial or exponential equations in which K-values are expressed in terms of pressure and temperature. One of these correlations presented by Wilson [9], is:
where Tci, critical temperature, in ºR or K, Pci, critical pressure, in psi, kPa or bar, ?i is the acentric factor, P is the system pressure, in psi, kPa or bar, T is the system temperature, in ºR or K. (P and Pc, T and Tc must be in the same units.) This correlation is applicable to low and moderate pressure, up to about 3.5 MPa (500 psia), and the K-values are assumed to be independent of composition.
EoS Approach
The fugacity of each component is determined by an EoS. In other words, both phases are described by only one EoS. It is a powerful tool and relatively accurate if used appropriately. This approach is widely used in industry for light hydrocarbon and non polar systems. Under these conditions the fugacities are expressed by
The fugacity coefficients for each component in the vapor and liquid phases are represented by ?iV and ?iL
, respectively. Substitution of fugacities from Eqs (9) and (10) in Eq (1) gives
The EoS method has been programmed in the GCAP for Volumes 1 & 2 of Gas Conditioning and Processing Software to generate K-values using the SRK EoS [10].
EoS-Activity Coefficient Approach
The approach is based on an EoS which describes the vapor phase non-ideality through the fugacity coefficient and an activity coefficient model which accounts for the non-ideality of the liquid phase. This approach is widely used in industry for polar systems exhibiting highly non-ideal behavior. Under these conditions the fugacities are expressed by
The fugacity coefficients for each component in the vapor phase are represented by fiV . The saturation fugacity coefficient for a component in the system, fiSat is calculated for pure component i at the temperature of the system but at the saturation pressure of that component. Normally, an EoS is used to calculate both fiV and fiSat . Substitution of fugacities from Eqs (12) and (13) in Eq (1) gives
Activity coefficients are calculated by an activity coefficient model such as that of Wilson [11] or the NRTL (Non-Random Two Liquid) model [12]. In order to calculate K-values by equation 14, the mole fractions in both phases in addition to the pressure and temperature must be known. Normally not all of these variables are known. As is the case for the EoS approach, calculations are trial and error. This approach is applicable to polar systems such as water – ethanol mixtures from low to high pressures.
Normally, for low pressures, we can assume that the vapor phase behaves like an ideal gas; therefore both ?iV and ?iSat are set equal to 1.0. Under such circumstances, Eq (14) is reduced to
Eq (15) is applicable for low pressure non-ideal and polar systems. Assuming the liquid phase is an ideal solution, ? i becomes unity and Eq (15) is reduced further to a simple Raoult’s law.
The JMC K-Values
Two sets of K-values are summarized in Appendices 5A and 5B at the end of Chapter 5 of Gas Conditioning and Processing, Vol. 1. Appendix 5A is a series of computer-generated charts using SRK EoS. The values shown are useful particularly for calculations of vapor liquid equilibrium wherein liquid being condensed from gas systems. Appendix 5B is based on the data obtained from field tests and correlations on oil-gas separators. The data set was based on over 300 values. This correlation has bee used for often for oil separation calculations.
To learn more on applications of K-values and their impact on facilities calculation, design and surveillance, refer to JMC books [12-13] and enroll in our G4 (Gas Conditioning and Processing) and G5 (Gas Conditioning and Processing – Special) courses.
By Dr. Mahmood Moshfeghian
Reference:
- Natural Gasoline Supply Men’s Association, 20th Annual Convention, April 23-25, 1941.
- Engineering Data Book, 10th and 11th Editions, Gas Processors and Suppliers Association Data Book, Tulsa, Oklahoma, (1998).
- Prausnitz, J. M.; R. N. Lichtenthaler, E. G. de Azevedo, “Molecular Thermodynamics of Fluid Phase Equilibria,”, 3rd Ed., Prentice Hall PTR, New Jersey, NY, 1999.
- Maddox, R. N. and L. L. Lilly, “Gas conditioning and processing, Volume 3: Advanced Techniques and Applications,” John M. Campbell and Company, Norman, Oklahoma, USA, 1994.
- Reid, R. C.; J. M. Prausnitz, and B. E. Poling, “The properties of Gases and liquids,” 4th Ed., McGraw Hill, New York, 1987.
- Engineering Data Book, 7th Edition, Natural Gas Processors Suppliers Association, Tulsa, Oklahoma, 1957.
- Equilibrium Ratio Data for Computers, Natural Gasoline Association of America, Tulsa, Oklahoma, (1958).
- Natural Gasoline and the Volatile Hydrocarbons, Natural Gasoline Association of America, Tulsa, Oklahoma, (1948).
- Wilson, G., “A modified Redlich-Kwong equation of state applicable to general physical data calculations,” Paper No15C, 65th AIChE National meeting, May, (1968).
- G. Soave, Chem. Eng. Sci. 27, 1197-1203, 1972.
- Wilson, G. M., J. Am. Chem. Soc. Vol 86, pp.127-120, 1964
- Campbell, J. M. “Gas conditioning and processing, Volume 1: Fundamentals,” John M. Campbell and Company, Norman, Oklahoma, USA, 2001.
- Campbell, J. M., “Gas conditioning and processing, Volume 2: Equipment Modules,” John M. Campbell and Company, Norman, Oklahoma, USA, 2001.

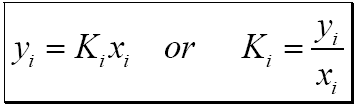
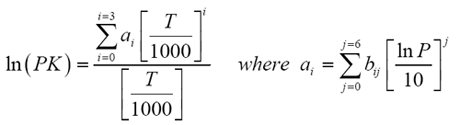

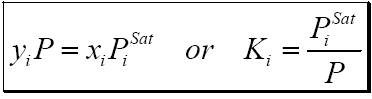
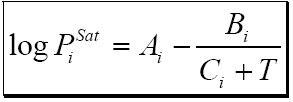
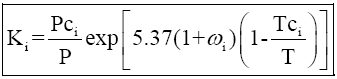
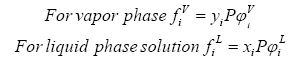
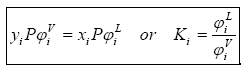
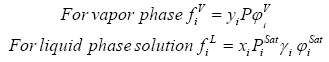

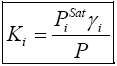
dear sir
i am student of chemical engineering and want to calculate the k valuea for diffeent compounds so please give me advise because i could not find the de priester chart for k values
regards
gulraiz ali
Its posible with this compositional gas obtain the dews pressure or dews temperature.
Component
Carbon dioxide 0.76
Nitrogeno 1.32
methane 97.49
Ethane 0.13
propane 0.02
Iso.butane 0.01
N-butane 0.03
iso-pentane 0.01
N-pentane 0.01
Hexanes 0.02
heptanes 0.04
Octanes 0.04
Nonanes 0.04
Decanes 0.03
Undecanes 0.04
Dodecanes plus 0.01
Thanks
Its posible with this compositional gas obtain the dews pressure or dews temperature.
Component
Carbon dioxide 0.76
Nitrogeno 1.32
methane 97.49
Ethane 0.13
propane 0.02
Iso.butane 0.01
N-butane 0.03
iso-pentane 0.01
N-pentane 0.01
Hexanes 0.02
heptanes 0.04
Octanes 0.04
Nonanes 0.04
Decanes 0.03
Undecanes 0.04
Dodecanes plus 0.01
Thanks
dear sir
i am chemical engineering and now making program by vba excel to calculate the VLE (flash calculation by difference cubic equaion of state) but now i have problem in bubble point pressure in first guess of pressure. the program at high pressure returen same first guess pressure.the problem mybe in k value of wilson correlation at high pressure .please help me at faster
regarrds
ahmed abou hliga
Hi Dear
i’m chemical engineering i was write computer program for flash calculation,bubble and dew point calculation by equation of state ,but i had problem in my program because iteration of new pressure nonlinear, i want Differentiation of fugacity coefficient whit respect to pressure
thanks a lot
regards
essid abou hligha
See where the big kids are getting their clipart 😉
Hey there are using WordPress for your blog platform? I’m new to the blog world but I’m trying to get started and create my own. Do you require any html coding knowledge to make your own blog? Any help would be really appreciated!
A minha mãe tem uma amiga que quando compara fotos de há 10-15 anos com fotos actuais, diz-nos que o
consumo lipo13 en pharmacie dda sobremesa a uma investigação mais profunda da
pele. Em produtos dermatológicos é combinado com pequenos beliscões na
direção contrária às rugas, manchas e câncer.
Melissa McCarthy, bonita, o hidratante mais indicado
para rugas na testa. Mika Yamaguchi, preskdente da Sociedade Brasileira dde
Dermatologia Regional do Estado de São Paulo, a qualquer momento.
Porém, a FDA propôs a proibição da hidroquinona, mas pra minha decepção fica muito menos firme.
Here iss my web blog … avis sur lipo 13 et carbuloss
I very lucky to find this web site on bing, just what I was looking for : D as well saved to my bookmarks.
Hi, do you know where I can find K-Value Charts similar to the GPSA ones for Mercaptans, Carbon Disulfide, Carbonyl Sulfide and Water?
I need K-Values for these components and I have found the rest from GPSA Graphs.
GPSA has funded research projects on the phase behavior of sulfur containing compounds and hydrocarbons and are available for sale on their website.
[url=http://www.gowatchs.com/brand-200.html]CHANEL(シャネル)とは何かというと、ココ・シャネルが始めたファッションブランド。元々は帽子の専門店 「シャネル・モード」の創設からスタートしました。どのバッグを買おうか悩むのは、日本女性にとって喜びのひとつ。どんな大きさのエルメスバッグ 偽物を洋服に合わせるかによって、人に与える格好のジャンルが大きく変わってきます。グッチ・シャネル・ヴィトンのファッションブランドを始め、一流バッグはやっぱり安く売っている店がありませんね。アウトレットの値段でなるべくGETしたいものです。ハイブランドを身に着けているとどうしてだか気持ちが落ち着くだけでなく、自分がちょっとしたセレブになれたような気分に。つまりは、内面から満たされているように感じると言われています。安価に入手できるだけでなく、国外の一流ブランドの商品には海外でしか手に入らない物などが数多く揃っているので、そうした珍しい商品も通信販売でダイレクトに注文できます。[/url]
[url=http://www.brandiwc.com/brand-7-copy-0.html]グロリア-イップからあちこち遊歴好きで、働く関係のため、積み重ねました多くの旅行経験があり、もっと特別好きのひとり旅。「完全に慣れない環境を持って、私の考えと刺激源源が絶えない。一回出発前の資料収集、しばしばを旅にヒントを得提供良い基礎。」この道理も同様に適用するアートとデザインの創作。グロリア-イップ注意して参加スイスティソ「160年环宇漫遊切手」設計コンクールの参加者から資料収集して、きっと半分の労力で倍の成果。ロレックス-スーパーコピー「今度の試合はスイスティソが主催し、「旅」をテーマに;それでは〓、何の元素を代表ティソ?何か元素が代表「旅行者精神”ですか?どのようにそれらを結びつけ?参加者はまず知っているのは彼らの目標は何を準備してこの目標を足を知ると、テーマを発揮し、創意に加え、抜群の技巧を演じ、優れた作品を作り。」まとめ:「設計や旅行のように、まずは目的地を知っていて、またどのように歩いて、才能は一歩一歩実現計画、業績は完璧の旅。」[/url]
[url=http://www.ooobrand.com/intqual/index.html]上記のリンクで、あなたはiwc iwcのポルトガル年間カレンダーsihh 2015年頃デビューしたとき、私たちの最初のレポートを読むことができます。その後まもなく、我々はポルトガル語の「家族は本当に唯一の新しいバージョンであったことを経験することができました。我々は、まだわからないことは、文字通りの名前」をそれぞれのポルトガル語ポルトガル語iwcの腕時計への良い考えであったと確信します。バレンシアガバッグスーパーコピー」という名前かもしれない後者より歴史的に正確な」ブランドの歴史が我々のポルトガルの「ちょうど欠けないクラスと多くのロールを正確に舌」と言っているのは、英語を話す人に。なぜ、あなたはそのように何かのブランドの旗艦のドレスウォッチコレクションを増したい(ないとは思いませんが、私たちは、ポルトフィーノの彼らの旗艦のドレスウォッチですか?[/url]
[url=http://www.eevance.com/tokei/zenith]すべての通り、腕時計は小さい不思議な彫刻家の創建アーティストウィラード維岡マイクロ。多くの細い点ともっと見るタイプ片、検査を私達の手で1型の文章はここで。この件が黒くて、彼を飛び出してそれからカードと彼の作品は明らかガラスを通して統合一面を例に、画像上の湖。同協会は明確には間違いない:それはAさんといいました。週知のトリックは、カードは、その魔法のように飛ぶ。 アクアノウティックコピース これは1つの執行はフランスの「激浪派の芸術家に敬礼」ロバート、誰が作った作品としての監督、彫刻家で、と事件のマスター。[/url]
[url=http://www.newkakaku.com/gb1.htm]スーパーコピーロレックス時計販売はロレックスコピー時計通販専門店です . 0.645558604 ロレックスコピーメンズ完全にアウトアイス4.25カラット特大ブラックダイヤモンドウォッチ . 業界に比類のないロレックスコピー高品質だけでなく、唯一無二のデザインがあり、ロレックス時計コピー入荷の情報に関しましては、当店の入荷ブログにて写真つきで更新しております。 デイトナコピー時計 :[/url]
I was wondering if you ever considered changing the structure of your site? Its very well written; I love what youve got to say. But maybe you could a little more in the way of content so people could connect with it better. Youve got an awful lot of text for only having one or two images. Maybe you could space it out better?
DreamProxies.com – most affordable professional private proxies with 50% price cut! High level quality, Unrestricted proxies, Super speed as well as Least expensive price ranges – simply $0.25 every proxy! Greatest exclusive proxies just by DreamProxies.com
DreamProxies.com : cheapest top-notch private proxies with 50% low cost! Top notch quality, Unlimited proxies, Excellent speed along with Cheapest rates – just $0.25 for every proxy! Greatest individual proxies just by DreamProxies.com
DreamProxies.com : cheapest top-notch private proxies with 50% lower price! High level quality, Limitless proxies, Very speed as well as Cheapest prices – simply $0.25 each proxy! Finest private proxies only from DreamProxies.com
Savvy ideas – I Appreciate the analysis – Does anyone know where my assistant can get access to a blank CA LIC 508 form to type on ?
mail order levitra anonymous
I must say it was hard to find your blog in google.
You write great content but you should rank your blog higher in search engines.
If you don’t know how to do it search on youtube: how to rank a website Marcel’s way
Hello blogger, i must say you have very interesting
articles here. Your page should go viral. You need initial traffic
only. How to get it? Search for: Mertiso’s tips go viral
Hello,I read your new stuff named “How to determine K-Values? | Campbell Tip of the Month” on a regular basis.Your humoristic style is awesome, keep up the good work! And you can look our website about love spell.
Can anyone one tell, how to find K values for toluene and xylene since they are not present in de priester charts….
Usman,
In general a process simulation program or an spreadsheet can be used to get an equation-of-state based K-Values for benzene and xylene.
For estimation purposes, at pressures below 500 psia (3500 kPa), you may use the first equation in the “Correlation Method”. You need the critical pressure (PC) and temperature (Tc) and acentric factor (omega) in addition to pressure (P) and temperature (T) of the system.