In the previous “Tip of the Month” we briefly discussed the importance of liquid density for process simulation and equipment design and introduced different methods of their predictions. In addition to direct laboratory measurement, three different methods were introduced to compute liquid density. The methods were (a) charts and monographs, (b) correlations and (c) EoS or volume translated EoS.
In this “Tip of the Month”, we will present a comparison between accuracy of different correlations and EoS methods. The focus will be on correlations for light hydrocarbons which have wider applications in industry.
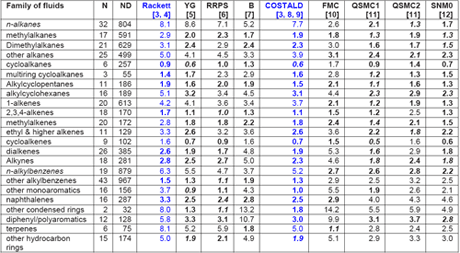
Recently, Mulero et al. [1] have evaluated nine empirical correlations for their accuracy and applicability in calculation of the liquid saturation density of pure fluids. All of them were based on the corresponding states principle, and they have included very recent correlations. One model required only the knowledge of critical parameters, but most of them needed the critical parameters and acentric factor as inputs, and one required the Lennard-Jones molecular parameters and the acentric factor as input data. As a reference, they took the numerical values for the liquid saturation density accepted by the DIPPR [2] project for 552 fluids, grouped into 30 families. Recommendations are given for the use of each model and for the choice of the adequate model for each family of fluids, including for particular fluids. For detail comparison and suggestions, the readers are referred to their paper; however, Table 1 is a summary of their comparison for pure fluids. The two most common correlations in gas industry, Rackett and COSTALD (highlighted in blue color) are also discussed in Chapter 3 of JMC Volume 1 of Gas Conditioning and Processing Book [3].
Table 1: MAPDs (Mean value of Absolute Percent Deviations) of the Calculated Liquid Saturation Densities for Several Families of Fluids with Respect to the DIPPR [2] Data when Using Correlationsa-c [1]
The numbers in italics represent the lowest MAPDs, and the numbers in bold show MAPDs that are similar (1%) to the lowest one. b YG) Yamada and Gunn; RRPS ) Reid et al.; B) Bhirud; QSMC1) Queimada et al.; QSMC2) Queimada et al.; SNM0) Mchaweh et al.; FMC) Fau´ndez et al.. c N) number of fluids, ND) number of data.
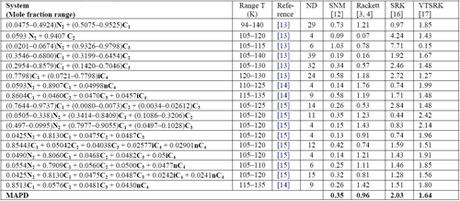
Similarly, Mchaweh et al. [12] reported the results of comparison study for light hydrocarbon mixtures containing nitrogen. A summary of their work is presented in Table 2. Their evaluation did not include COSALD; however, our experience indicates that COSTALD MAPD is below 0.5 %. It should be noted that even though Volume Translated SRK (VTSRK) improves the accuracy of the SRK EoS but still is not good enough for industrial applications.
Table 2: The MAPD for 17 multi-component low temperature systems (226 data points) using different method [12]
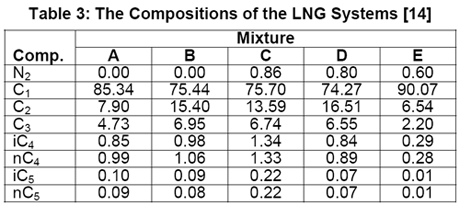
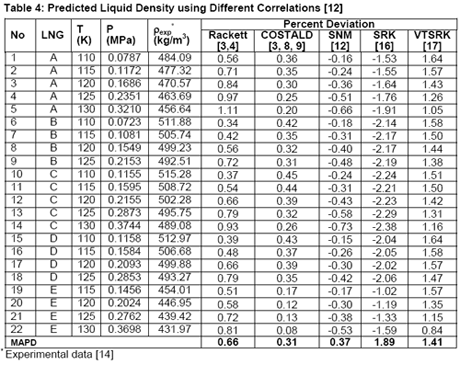
In another paper, Javanmardi et al. [18] evaluated several correlations and EoSs for prediction of LNG density. Among others, five LNG mixtures consisting of 22 experimental data were studied. The compositions of these LNG mixtures are presented in Table 3 and a summary of comparison between accuracies of different methods is shown in Table 4.
Analysis of Tables 1 through 4 indicates that, for pure compounds, the SNM [12] in general gives better accuracies. However, for light hydrocarbon mixtures (NGL and LNG) liquid densities prediction, it is highly recommended to use COSTALD [3, 8, 9] even though SNM correlation also give accurate and compatible results. The SRK [16] and its volume translated correction (VTSRK, [17]) accuracies are not as good as the correlations so their use for practical applications must be done with care and caution. Needless to point out that SRK predict gas densities accurately. Based on our experiences and similar observations, we have programmed, in the JMC GCAP software, SRK for gas and COSTALD for liquid densities.
In next “Tip of the Month” we will provide Part 2 of guidelines for proper use of commercial simulator to calculate liquid densities.
To learn more about liquid density and its impact on facilities calculation, design and surveillance, refer to JMC books and enroll in our G4 (Gas Conditioning and Processing) and G5 (Gas Conditioning and Processing – Special) courses.
By Dr. Mahmood Moshfeghian
Reference:
- Mulero, A., Cachadina, I. and Parra, M. I., “Liquid Saturation Density from Predictive Correlations Based on the Corresponding States Principle. Part 1: Results for 30 Families of Fluids,” Ind. Eng. Chem. Res., 45, 1840-1848, 2006
- DIPPR (Design Institute for Physical Property Data) files, Version 17.0; American Institute of Chemical Engineers: New York, 2003 (supplied by Technical Database Services, Inc., www.tds.cc).
- Campbell, J. M. “Gas conditioning and processing, Volume 1: Fundamentals,” John M. Campbell and Company, Norman, Oklahoma, USA, 2001.
- Rackett, H. G. Equation of state for saturated liquids. J. Chem. Eng. Data, 15, 514, 1970 5. Yamada, T.; Gunn, R. D. Saturated liquid molar volumes: The Racket equation. J. Chem. Eng. Data, 18, 234, 1973
- Reid, R. C.; Prausnitz, J. M.; Sherwood, T. K. The Properties of Gases and Liquids; McGraw-Hill: New York, 1977.
- Bhirud, V. L. A four-parameter corresponding states theory: Saturated liquid densities of anormal fluids. AIChE J., 24, 1127, 1978.
- Hankinson, R. W.; Thomson, G. H. A new correlation for saturated densities of liquids and their mixtures. AIChE J. 1979, 25, 653.
- Thomson, G. H.; Brobst, K. R.; Hankinson, R. W. An improved correlation for densities of compressed liquids and liquid mixtures. AIChE J., 28, 671, 1982
- Faundez, C. A.; Mulero, A.; Cuadros, F. Molecular Thermodynamic Models for the Vapour-Liquids Equilibrium of Non-Polar Fluids. J.. Phase Equilib., 21, 364, 2000.
- Queimada, A. J.; Stenby, E. H.; Marrucho, I. M.; Coutinho, J. A. P. A new corresponding states model for the estimation of thermophysical properties of long chain n-alkanes. Fluid Phase Equilib., 212, 303, 2003.
- Mchaweh, A.; Alsaygh, A.; Nasrifar, Kh.; Moshfeghian, M. A simplified method for calculating saturated liquid densities. Fluid Phase Equilib., 224, 157, 2004.
- M.J. Hiza, W.M. Haynes, W.R. Parrish, J. Chem. Thermodyn. 9, 873–896, 1977.
- Haynes, W. M., Measurements of Orthobaric-Liquid Densities of Multicomponent Mixtures of LNG components Between 110 and 130 K, J. Chem. Thermodynamics, 14, 603-612, 1982.
- M.J. Hiza, W.M. Haynes, J. Chem. Thermodyn. 1, 1–10, 1980.
- Soave, G., Chem. Eng. Sci., vol. 27, 1197-1203, 1972.
- Peneloux, A. E., Rauzy, E., and Freze, R., Fluid Phase Equilib., Vol. 8, 7-23, 1982.
- Javanmardi, J., Nasrifar, Kh., Moshfeghian, M., Comparing different methods for prediction of liquefied natural gas densities, Engineering Journal of the University of Qatar, Vol. 18, 39-56, 2005

Hello,
If i want to calculate the density (liquid) of ethane. Beetween – 70 to -100 degC. How do i proceed?
Thanks in advance.
Agne Myhre