Introduction
Engineers are frequently asked to calculate the fluid pressure drop in a piping system. Many software programs are available for solving complicated hydraulic problems; however’ they can be complex and difficult to use. In addition, there are many tables or shortcut methods that give adequate answers but they usually apply to predefined conditions which are sometimes misleading or less accurate. This “Tip of the Month” discusses a method of calculating friction pressure losses for liquid lines. A spreadsheet is presented that gives friction losses based on this method.
Background Information
Equation 1 is known as the Darcy-Weisbach (sometimes called the Darcy) equation and has been used by engineers for over 100 years to calculate fluid flow pressure loss in pipe. This equation is derived by dimensional analysis and relates the various parameters that contribute to the friction loss. A correction factor, called the Moody friction factor, is included which compensate theoretical results with the experimental results.

Where:
hL = Head loss due to friction, m [ft]
f = Moody friction factor
L = Pipe length, m [ft]
V = Velocity, m/s [ft/sec]
g = Gravitational acceleration, 9.81 m/sec2 [32.2 ft/sec2]
D = Inside diameter, m [ft]
The task of determining the friction factor can be difficult due to the many variables that influence flow behavior. For example, the friction factor is significantly different if the fluid flow exhibits Newtonian or non-Newtonian behavior, or if the flow is laminar or turbulent. Other variables that influence the friction factor are properties of the pipe represented by absolute roughness and inside diameter, and fluid parameters such as flow rate, viscosity and density.
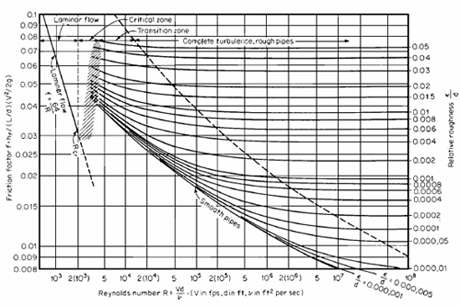
The Moody diagram given in Figure 1 is a classical representation of the fluid behavior of Newtonian fluids and is used throughout industry to predict fluid flow losses. It graphically represents the various factors used to determine the friction factor. For example, fluids with a Reynolds number of 2000 and less, the flow behavior is considered a stable laminar fluid, and the friction factor is only dependent on the Reynolds number. The friction factor for the Laminar Zone is represented by Equation 2. Fluids with a Reynolds number between 2000 and 4000 are considered unstable and can exhibit either laminar or turbulent behavior. This region commonly referred to as the Critical Zone, and the friction factor can be difficult to accurately predict. Judgment should be used if accurate predictions of fluid loss are required in this region. Either Equation 2 or 3 are commonly used in the Critical Zone. Beyond 4000, the fluid is considered turbulent and the friction factor is dependent on the Reynolds number and relative roughness. For Reynolds numbers beyond 4000, the Moody diagram identifies two regions, Transition Zone and Completely Turbulent Zone. The friction factor represented in this region is given by Equation 3.
Figure 1. Moody Friction Factor Diagram
Where:
Re = Reynolds Number
V = Fluid velocity, m/s [ft/sec]
D = Inside diameter, m [ft]
e = absolute pipe roughness, m [ft]
? = Fluid density, kg/m3 [lbm/ft3]
µ = Fluid viscosity, kg/(m-s) [lbm/(ft-sec)]
The Method
The Colebrook formula, Equation 3, is used throughout industry and accurately represents the Transition and Turbulent flow regions of the Moody Diagram. However, this implicit equation is difficult to solve by manual methods. Typically an iterative method is used to solve the Colebrook equation. One method of solving this equation is with numerical analysis technique called Newton-Raphson’s1 Method. This successive approximation approach is represented by Equation 5, and involves 1) the Colebrook formula, 2) the first derivative of the Colebrook formula and 3) an initial guess. Since the Colebrook formula is a convergent equation, the solution is usually determined with less than four iterations.
Where:
fn = nth iteration friction factor
fn+1 = (n+1)th iteration friction factor
g(fn) = Colebrook equation
g'(fn) = First derivative of Colebrook equation
A macro that solves the Colebrook formula is given in this spreadsheet. It is easily adapted to programmable calculators. The iterative method assumes that the following input variables are available:
Pipe inside diameter – mm [in]
Pipe length – m [ft]
Absolute roughness – m [ft]
Absolute viscosity – cP
Fluid relative density
Fluid flowrate – m3/h [gpm]
Example Problem
The macro begins with inputting the variables needed to solve for the Moody friction factor. Next, the macro determines the Reynolds Number. If the Reynolds value is below 2000 the flow is considered laminar and a simplified friction formula shown in Equation 2 is used. Above 2000 the flow is considered turbulent and the Colebrook formula is used. Finally, the Moody friction factor is determined and combined with the Darcy formula, Equation 1, to determine the fluid friction losses.
Numerous results were checked against values given in “Cameron Hydraulic Data Book”2 and found to vary by less than one percent. A term called “Delta-F” is also given in the spreadsheet which gives an indication of the variance in the Colebrook equation and the calculated value. Values of Delta-F less then 0.05 indicates an accuracy of three or more decimal places.
Alternate Method:
An alternate method of determining the friction factor is given by Chen3. His method of calculating the friction factor is explicit and does not require iterations to solve. This method has been by studied by Gregory and Fogarasi4, and found to give satisfactory values compared to the Colebrook equation. For those interested in this alternate approach, see Equation 6.
Where:
f = Fanning friction factor (1/4 of Moody friction factor)
D = Inside diameter, m [ft]
e = absolute pipe roughness, m [ft]
Re = Reynolds Number
To learn more about friction factor and its impact on piping and pipeline calculation, design and surveillance, refer to JMC books and enroll in our ME41, PL4, PL61, and G4 courses.
By: Joe Honeywell
Instructor & Consultant
References:
- “Elementary Numerical Analysis”, by S. D. Conte, McGraw-Hill Book Company, 1965, pp 30
- “Cameron Hydraulic Data Book”, by Ingersoll-Rand Company, Woodcliff, N. J., 15 ed., pp 3-49 to 3-85
- Chen, N.H., An Explicit Equation for Friction Factor in Pipe, Ind. Eng. Chem. Fund., 18, 296,1979
- Gregory, G.A. and Fogarasi, F., Alternate to Standard Friction Factor Equation, Oil & Gas Jour. Apr. 1 1985, pp 127.
Excel Program Input and Output

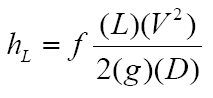
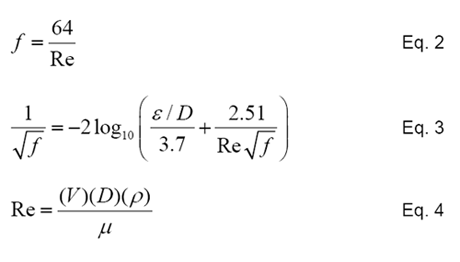


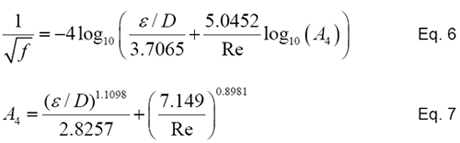


How can I get the spreadsheet?
Hello, I also want to know, how could I get a spreadsheet? Thanks very much!
I need the spreadsheet for quick calculation
how did you arrive at 526.76 m^3/h = 310 GPM?
310 GPM = 70.4 m^3/h
Please send the excel formula sheet. This would speed up my calcs. Thanks you very much.
Tony Gawrysiak
Technical Manager
ComfortPro Systems
Can you please send me the spreadsheet for friction pressure drop calculation? Thank you.
Can you please send me the spreadsheet for friction pressure drop calculation? Thank you.
Can you please send me the spreadsheet for friction pressure drop calculation? Thank you.
please send me the spread sheet to :sarada.vasireddy@gmail.com
Por favor hoja de calculo
enviarme a charleeinc@hotmail.es y muchas gracias
Could I please get the spreadsheet for calculations?
Jordan.a.whetsell-1@ou.edu
Where can I download the Friction Pressure Drop Calculation
Can you please send me the spreadsheet ?
Can you please send me the spreadsheet for friction pressure drop calculations? Thank you very much.
Thank you!
Can you please send me a copy of the spreadsheet that you referred to? Thanks!
Hey very interesting blog!
My webpage … 24 hour ac repair 19107
Fastidious respond in return of this question with genuine arguments and describing the whole thing regarding
that.
Also visit my site; sky broadband help telephone number
It’s going to be finish of mine day, but before end I am reading this great article to increase my knowledge.
Look into my webpage; you could try here (crawfordmwel.centerblog.net)
Magnificent goods from you, man. I’ve understand your stuff previous to and you’re just extremely wonderful.
I actually like what you have acquired here, certainly like what you are saying and the way in which you say it.
You make it enjoyable and you still care for to keep it sensible.
I can not wait to read much more from you. This is actually
a great site.
This will be a excellent web site, might you be interested in doing an interview regarding how you created it? If so e-mail me!
Hi Sr. very good note, please can i get the spread sheet jony_cosacurio@yahoo.com
Interesting article and comparisons. I also would like the spread sheet calculator; but, wonder if there is one for gas flow or what are the factors that need to be changed for gas production considerations.
this program very important to me please send this program
DreamProxies.com — cheapest high level private proxies with 50% low cost! Elite quality, Limitless proxies, Extremely speed and Cheapest price ranges : just $0.25 every proxy! Finest non-public proxies simply from DreamProxies.com
Will you please send me a copy of your spreadsheet?
It will greatly help me with my calculations.
Thanks a lot for your help!!
Will you please send me a copy of your spreadsheet?
Will you please send me a copy of your spreadsheet?
” I am unsure where you’re getting your information, nevertheless great topic. I must spend some time learning or understanding more. Thank you for fantastic information. I was trying to find this information. “
Hello Joe, is it possible for you to send me the spreadsheet for a quick calculation? I would appreciate it. My email is tati_3217@hotmail.com
Will there be a part 2 some time in the future? I simply have to tell you that your pages are really awesome. I was walking on the beach on Monday when I discovered your blog. Some really excellent information here. Try to make the guest blog as awesome as possible by promoting and dropping links. Wow, that is unbelievable.