The formation of hydrates in processing facilities and pipelines has been a problem to the natural gas industry. Whether the problem occurs in transportation or processing, hydrate formation can cause shutdowns and even destruction of valuable equipment. Because of these devastating and often costly consequences of hydrate formation, methods have been applied to prevent hydrate development in gas streams. The conditions that tend to promote hydrate formation include: low temperature, high pressure, and a gas at or below its water dew point temperature with “free” water present. The formation of hydrates can be prevented by using any of the following techniques; (a) adjusting the temperature above and pressure below the hydrate formation condition, which may not be practically possible due to economical and/or operational reasons, (b) dehydrating a gas stream with solid desiccant or glycol dehydration to prevent a free water phase, and (c) impeding hydrate formation in the free water phase by injection of an inhibitor. The most common inhibitors are methanol (MeOH), monoethylene glycol (MEG) and diethylene glycol (DEG). Typically, methanol is used in a non-regenerable system while MEG and DEG are used in regenerable processes. With the use of inhibitors, the injected inhibitor may distribute into three possible phases: (a) the vapor hydrocarbon phase, (b) the liquid hydrocarbon phase and (c) the aqueous phase in which the hydrate inhibition occurs and the inhibitor has an effect on hydrate formation inhibition. Therefore, calculating the inhibitor concentration in aqueous phase is important.
Several models have been developed for prediction of hydrate formation condition in the presence of an inhibitor. Hammerschmidt [1], Nielsen and Bucklin [2], Carroll [3] and Moshfeghian-Maddox [4] correlations are used to predict concentration of inhibitors in an aqueous solution and for lowering the hydrate formation temperature. Portability and simplicity are advantages of these correlations since they are applicable even with a simple calculator and the results are in good agreement with the experimental data [1-4]. It is to be noted that simulation packages such as ProMax® [5], HYSYS® [6] and GCAP [7] are available for predicting the effect of inhibitors on hydrate formation.
The injection rate is a function of feed gas temperature (FGT), pressure (FGP), relative density (SG), hydrate formation temperature depression (HFTD), and lean solution concentration. Recently, Moshfeghian and Taraf [8-10] proposed a shortcut/graphical method to predict the required MEG or MeOH weight percent and flowrate for a desired depression in hydrate temperature of natural gas mixtures.
In this tip of the month (TOTM), we will demonstrate how the diagrams presented by Moshfeghian and Taraf [10] can be used to determine the concentration of MeOH in the rich solution and the required total injection rate for a desired hydrate formation temperature.
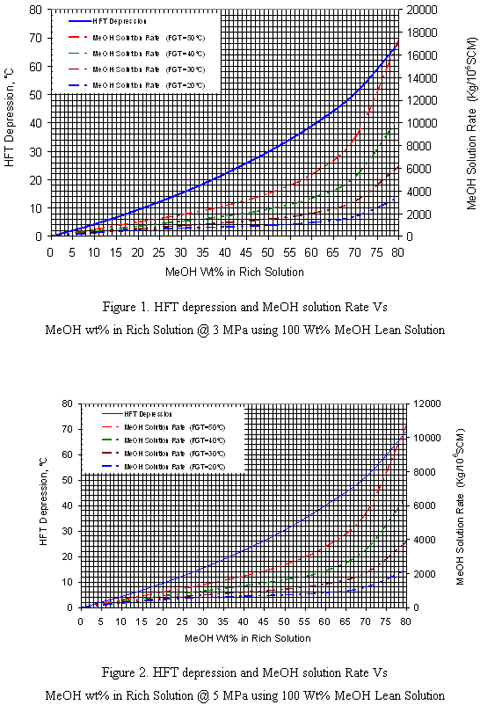
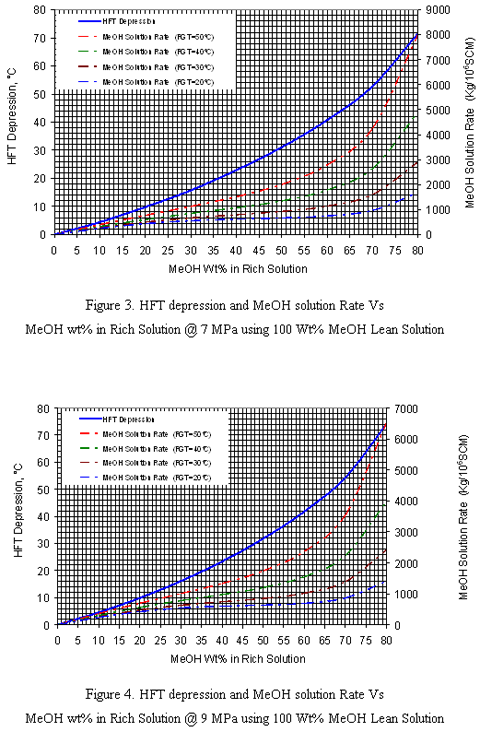
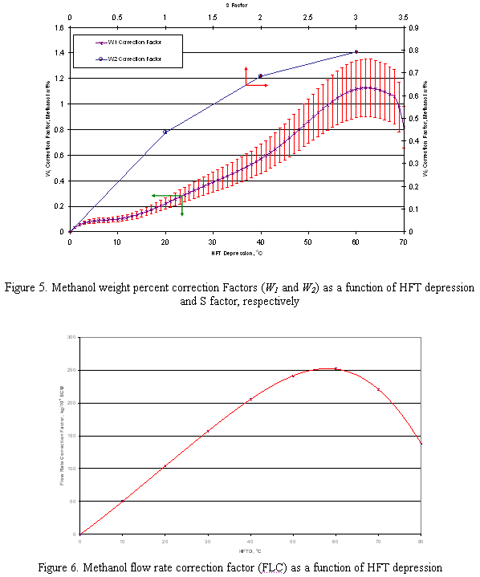
Figures 1-4 are applicable for any wet natural gas mixture with specific gravity of 0.6. Note that the right hand y-axis represents the total injection rate of MeOH which may distribute into gas phase, liquid hydrocarbon phase and rich solution phase. In order to extend the application of these charts to gas mixtures with other specific gravities, two correction factors and W2 should be used. These correction factors are used to correct the inhibitor concentration in the rich solution for other relative densities (0.65-0.80) which are shown in Figure 5. is the correction factor due to the difference of inhibitor concentration in the rich solution in different hydrate formation temperature depression. This factor is applicable for gas with specific gravities greater than 0.6. W2 is the correction factor due to the difference in inhibitor concentration in the rich solution due to the difference in gas specific gravities. To determine W2, the S-factor is defined as follow:
By calculating the S-factor, W2 can be easily read from Figure 5. This correction factor is applicable for gas with specific gravities of 0.65 and greater.
Using W1 and W2, the obtained weight percent from Figures 1-4 (Wtfig) is corrected as follows:
The obtained flow rate from charts (Figures 1-4) should be corrected further using flow rate correction factor (FLC) presented in Figure 6. The correction factor can be applied as follow:
Considering the above correction factors, the charts are applicable for natural wet gases with specific gravities of 0.6-0.8 saturated, at temperature of 20, 30, 40 and 50 oC and pressures of 3, 5, 7 and 9 MPa.
As mentioned earlier, the inhibitor in the aqueous phase (rich solution) has an effect on hydrate formation inhibition and it is independent of the inhibitor weight percent in the lean solution. The same hydrate temperature depression is achieved when there is a similar inhibitor weight percent in the rich solution. However, the injection rate is a function of both lean and rich stream concentration.
Therefore, a simple material balance gives the following equation:
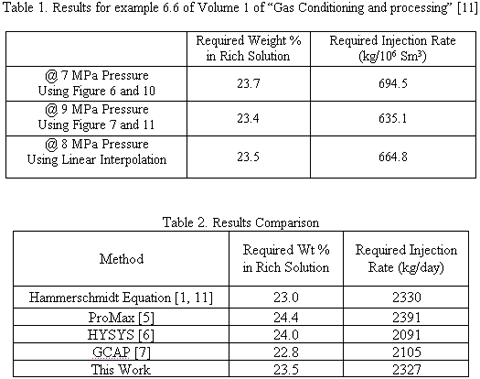
To demonstrate the application of the proposed charts, example 6.6 in Volume 1 of “Gas Conditioning and Processing,” [11] is considered. In this example it is stated that 3.5 × 106 Sm3/d of natural gas leaves an offshore platform at 40 oC and 8000 kPa. The hydrate temperature of the gas is 17 oC. The gas arrives onshore at 5 oC and 6500 kPa. The associated condensate production is 60 m3/106 Sm3. The amount of methanol required to prevent hydrate formation in the pipeline is to be estimated.
It should be noted that in this example the composition (or relative density) of natural gas is not given; therefore, to demonstrate the use of these charts a relative density of 0.6 is assumed. The feed gas pressure is 8 MPa so a linear interpolation between 7MPa (Figure 3) and 9 MPa (Figure 4) is applied.
The summary of known data is:
FGT = 40 oC; HFT = 17 oC, FGP = 8 MPa, SG = 0.60, Inhibitor = 100 Wt % MeOH
Minimum Flowing Temperature (MFT) = 5 oC
HFTD = HFT – MFT = 17 – 5 = 12 oC
Due to the uncertainties involved in all inhibitor injection calculation methods, a safety factor is normally applied to the hydrate formation temperature depression. For example, this case has the HFTD set to the minimum flowing temperature. In practical situations, a design factor such as 5 deg oF (2.8 oC) below the minimum flowing temperature is used to ensure any errors in the estimation method are covered, and also to ensure that the minimum temperature includes any upset process condition.
As an example, the location of HFTD, required weight percent and injection rate of MeOH for pressure of 9 MPa for this example are shown in Figure 4. The results are tabulated in Table 1, and a comparison between the results of this work and those based on the Hammerschmidt [11] equation, ProMax [5], HYSYS [6], and GCAP [7] is shown in Table 2. As can be seen from Table 2, the agreement between the graphical method and ProMax is quite good. The methanol injection rates as estimated by HYSYS are significantly lower than the other methods, and caution should be applied if one is using HYSYS for inhibitor injection estimates. It is likely that the differences in the natural gas water dew point predictions are the result of this discrepancy. Also note for modeling methanol liquid systems in process simulators, a polar equation of state package for the vapor phase and a polar model for the liquid phases must be selected to obtain accurate results.
Conclusions
For determination of required methanol concentrations in the aqueous phase (rich solution) and its flowrate for a desired depression in hydrate formation temperature of a wet natural gas mixture, reference charts proposed by Moshfeghian and Taraf [10] can be used. These charts were generated for pressures 3, 5, 7, and 9 MPa based on ProMax and are generated for a natural gas mixture with relative density of 0.6 but are extended to gases with relative densities up to 0.8 by using two correction factors. A simple equation was also proposed to extend the charts’ usage to other lean MeOH concentrations.
The results obtained by these charts are compared with the results of the other methods for a practical case and good agreement is found. It is also suggested that linear interpolation can be used for pressures between 3, 5, 7, and 9 MPa.
To learn more about similar cases and how to minimize operational problems, we suggest attending our PL4 (Fundamental Pipeline Engineering), G4 (Gas Conditioning and Processing) and G5 (Gas Conditioning and Processing – Special), courses.
To receive the full manuscript of Moshfeghian-Taraf’s paper, send an e-mail to info@jmcampbell.com
By: Dr. Mahmood Moshfeghian
Check it out, interesting conversation going on on process safety.
REFERENCES
- Hammerschmidt, E.G., “Formation of gas hydrates in natural gas transmission lines”, Ind. & Eng. Chem., Vol: 26, p. 851, 1943.
- Nielsen, R. B. and R.W. Bucklin, “Why not use methanol for hydrate control”, Hydrocarbon Processing, Vol: 62, No. 4, P 71, April 1983.
- Carroll, J., “Natural Gas Hydrates, A Guide for Engineers”, Gulf Professional Publishing, 2003.
- Moshfeghian, M. and R. N. Maddox, “Method predicts hydrates for high-pressure gas stream”, Oil and Gas J., August 1993.
- ProMax®, Bryan Research & Engineering Inc, Version 2.0, Bryan, Texas, 2007
- HYSYS® v 2006, Aspen Technology Inc., Cambridge, Massachusetts, 2006
- GCAP®, 8th Ed., Facilities Analysis Software, John M. Campbell & Co., Norman, Oklahoma, 2009.
- Moshfeghian, M. and Taraf, R., “New method yields MEG injection rate”. Oil and Gas J., September 2008.
- Moshfeghian, M. and Taraf, R., “A new shortcut/graphical method to determine the required MEG injection rate for natural gas hydrate inhibition,” 87th Annual Gas Processor Association Convention March 2-5, in Grapevine, Texas, (2008).
- Moshfeghian, M. and Taraf, R., “Generalized Graphical Method to Determine the Required MEG and Methanol Injection Rate for Natural-Gas Hydrate Inhibition,” 88th Annual Gas Processor Association Convention March 8-11, in San Antonio, Texas, (2009).
- Campbell, J. M., “Gas Conditioning and Processing”, Vol. 1, The Basic Principles, 7th Ed., Second Printing, J. M. Campbell and Company, Norman, Oklahoma, 1994.


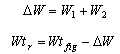
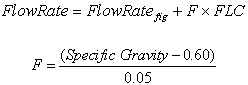


This is very useful information and highly educative for practicing engineers, however, case study for numerical applications in the industry is not clear as such as explained below. Your help and guidance is appreciated.
Tables 1 in this case study make use of Figure 6 and 10 for 7 MPa Pressure case and Use Figure 7 & 11 for 9 MPa case, but these Figures are not included in this publication, please let me have them.
Otherwise if we use given figures, 3 & 4 with case study, for HFT Depression of 12 C, duly calculated by the author, then we get very different results. Kindly elaborate. Thanks
i really like this information it has helped me with my day to day work since I deal with these facts every day
Greate pieces. Keep writing such kind of information on your site.
Im really impressed by your site.
Hi there, You have performed an incredible job.
I’ll definitely digg it and for my part recommend to my friends. I’m sure they’ll be benefited from this website.
Hi, i feel that i noticed you visited my weblog so i got here to go back the choose?
.I’m trying to in finding issues to enhance my site!I assume its ok to make use of some of your ideas!!
I do not even know the way I stopped up right here, but I assumed this
publish was once great. I do not know who you might be however certainly you’re going to a famous blogger when you aren’t already.
Cheers!
You really make it seem so easy with your presentation but I in finding this matter to be really something that
I feel I might by no means understand. It kind of feels too
complex and very extensive for me. I’m looking forward for your next put up, I’ll attempt to get the dangle of it!
Also visit my site: certified toyota repair shop
Along with the whole thing that appears to be developing throughout this particular subject matter, many of your points of view tend to be relatively exciting. Even so, I appologize, because I do not subscribe to your entire idea, all be it refreshing none the less. It would seem to everybody that your comments are not entirely rationalized and in actuality you are yourself not really wholly confident of your assertion. In any case I did enjoy reading it.
Throughout the great scheme of things you receive an A for hard work. Where you actually lost me was first in all the particulars. You know, it is said, the devil is in the details… And it could not be more accurate here. Having said that, permit me say to you what did deliver the results. Your authoring is extremely persuasive which is probably the reason why I am making an effort in order to opine. I do not make it a regular habit of doing that. 2nd, whilst I can easily notice the jumps in reason you come up with, I am not necessarily certain of how you seem to connect the points which in turn make your final result. For the moment I will, no doubt yield to your issue but wish in the foreseeable future you connect the facts better.
Very good site you have here but I was curious if you knew of any user discussion forums that cover the same topics talked about in this article? I’d really like to be a part of online community where I can get feedback from other experienced individuals that share the same interest. If you have any suggestions, please let me know. Bless you!
I must say you have hi quality articles here. Your posts can go viral.
You need initial traffic only. How to get massive traffic?
Search for; Murgrabia’s tools go viral
Can I simply say what a aid to search out somebody who truly is aware of what theyre speaking about on the internet. You definitely know easy methods to deliver an issue to gentle and make it important. More folks need to read this and understand this side of the story. I cant consider youre not more standard since you positively have the gift.
Espetacular! Você sabe usar as palavras. Amei seu artigo. Muito bem escrito! Parabéns mesmo!