How sensitive is pressure drop due to friction with roughness factor?

In the February 2007 tip of the month (TOTM), Joe Honeywell [1] presented a procedure for calculating fluid pressure drop for liquid in a piping system due to friction. Continuing Honeywell’s TOTM, we will outline procedures for calculation of friction losses in oil and gas pipelines. From an engineer’s point of view the question may arise “how sensitive is friction pressure drop with the wall roughness factor?” Of course the answer is “it depends”. To explain this answer quantitatively and qualitatively, we will study the effect of wall roughness factor for two case studies in this month’s TOTM. In the first case study, an oil pipeline with a flow rate of 0.313 m³/s (170,000 bbl/day) and in the second case, a natural gas pipeline with a flow rate of 22.913 Sm³/s (70 MMSCFD) will be studied and calculation results will be presented in tabular and graphical format.

Friction Factor
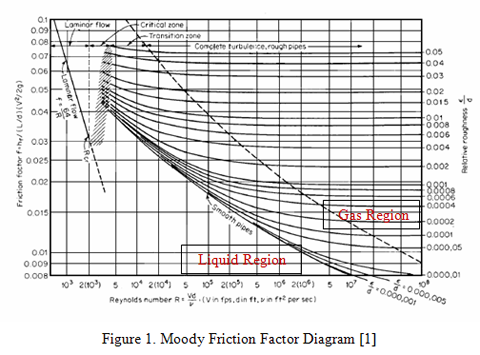
The Moody diagram in Figure 1 is a classical representation of the fluid behavior of Newtonian fluids and is used throughout industry to predict fluid flow losses.  It graphically represents the various factors used to determine the friction factor.  For example, for fluids with a Reynolds number of 2000 and less, the flow behavior is considered a stable laminar fluid and the friction factor is only dependent on the Reynolds number [2].  The friction factor, f, for the Laminar zone is represented by:

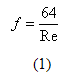
Where Re is the Reynolds number and is expressed as the ratio of inertia force to viscous force and mathematically presented as.

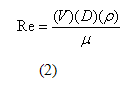
Fluids with a Reynolds number between 2000 and 4000 are considered unstable and can exhibit either laminar or turbulent behavior.  This region is commonly referred to as the critical zone and the friction factor can be difficult to accurately predict. Judgment should be used if accurate predictions of fluid loss are required in this region.  Either Equation 1 or 3 are commonly used in the critical zone.  If the Reynolds number is beyond 4000, the fluid is considered turbulent and the friction factor is dependent on the Reynolds number and relative roughness.  For Reynolds numbers beyond 4000, the Moody diagram identifies two regions, transition zone and completely turbulent zone. The friction factor represented in these regions is given by the Colebrook formula which is used throughout industry and accurately represents the transition and turbulent flow regions of the Moody diagram.

The Colebrook formula for Reynolds number over 4000 is given in equation 3.

The roughness factor is defined as the absolute roughness divided by the pipe diameter or . Typical values of absolute roughness are 5.9x10^-4 in (0.0015 mm) for PVC, drawn tubing, glass and 0.0018 in (0.045 mm) for commercial steel/welded steel and wrought iron [3].
The Colebrook equation has two terms.  The first term, ()/3.7, is dominate for gas flow where the Re is high.  The second term, , is dominate for fluid flow where the relative roughness lines converge (smooth pipes).  In the “Complete Turbulence” region, the lines are “flat”, meaning that they are independent of the Reynolds Number.  In the “transition Zone”, the lines are dependent on Re and .  When the lines converge in the “smooth zone” the fluid is independent of relative roughness.

Liquid (Incompressible) Flow
For liquid flow, equation 4 has been used by engineers for over 100 years to calculate the pressure drop in pipe due to friction. This equation relates the various parameters that contribute to the friction loss. This equation is the modified form of the Darcy-Weisbach formula which was derived by dimensional analysis.

The friction factor in this equation is calculated by equation 3 for a specified Reynolds number and roughness factor using an iterative method or a trial and error procedure.

Gas (Compressible) Flow
For gas flow, density is a strong function of pressure and temperature, and the gas density may vary considerably along the pipeline. Due to the variation of density, equation 5 should be used for calculation of friction pressure drop.

Again, the friction factor in this equation is calculated by equation 3 for a specified Reynolds number and roughness factor using a trial and error procedure. Actual volume flow rate is needed to calculate the velocity of gas in the line from which the Reynolds number is calculated. Equation 6 may be used to convert the volume flow rate at standard condition to the actual volume flow rate.

Case Study 1: Oil Pipeline
Consider a 16-inch (inside diameter of 395 mm) oil export line for transportation of 170,000 bbl/day (0.313 m³/s) of a 43 API crude oil (relative density of 0.81) from an offshore platform to the shore oil terminal. The total length of pipe is 55 km. The ambient temperature is 5 °C and the crude oil viscosity at the average pipe temperature is 0.001 cP. The pipe line inlet pressure is 14.9 MPa (absolute). Since the objective is to study the effect of roughness factor on friction pressure drop, we will ignore elevation change.
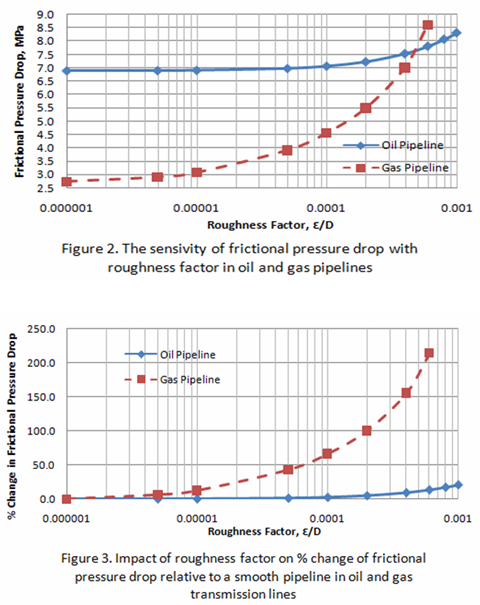
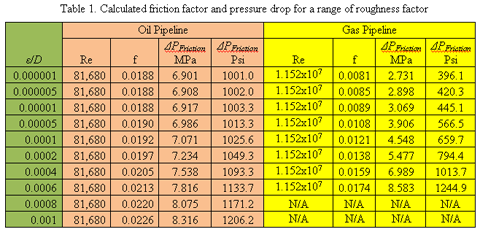
To study the effect of roughness factor on friction pressure drop, was varied from 1x10^-6 to 1x10^-3. The roughness factor of  = 1x10^-6 represents a very smooth pipe. The calculated friction pressure drop as a function of the roughness factor is plotted in Figure 2. For each value of roughness factor, the percent change in frictional pressure drop was calculated in comparison to a very smooth pipe ( = 1x10^-6) and the results are presented in Figure 3. The calculated results are also presented in Table 1.

Case Study 2: Gas Pipeline
Let’s consider an 8-inch (inside diameter of 190 mm) gas export line for transportation of 70 MMSCFD (22.913 Sm³/s) of natural gas with a molecular weight of 19.3 (relative density of 0.67) from an offshore platform to the shore. The total length of pipe is 43 km. The ambient temperature is 5°C and the gas viscosity at the average pipeline temperature is 1.1x10^-6 cP. The gas inlet temperature is 35°C and pressure is 13.0 MPa (absolute). Since the objective is to study the effect of roughness factor on friction pressure drop, we will again ignore elevation change.
Similar to the oil pipeline, the roughness factor, was varied from 1×10^-6 to 0.006. Note, for a roughness factor greater than 0.006, a higher inlet pressure, a larger diameter or lower flow rate was needed. The calculated friction pressure drop as a function of roughness factor is presented in Figure 2. For each value of roughness factor, the percent change in frictional pressure drop in comparison to a very smooth pipe ( = 1×10^-6) was calculated and the results are presented in Figure 3.

Discussion and Conclusions
The analysis of Figure 2 indicates that for the oil pipeline, the friction pressure drop is almost independent of the roughness factor in the range of 1×10^-6< <1×10^-4; however, for >1×10^-4, it will increase with . For liquid lines, the Reynolds number is normally in the range of 5×10⁴ to 1×10⁶. For this range, the friction factor curves in Figure 1 approach close to each other so the values of friction factors become close to each other.
Contrary to the oil pipeline, the friction pressure drop for the gas pipeline is a strong function of . As can be seen in Figure 2, friction pressure drop increases very rapidly with the roughness factor. Figure 3 shows the comparison of percent change of friction pressure drop between oil and gas pipelines as a function of roughness factor. For the liquid pipeline, the maximum change is 20 % but for the gas pipeline the maximum change is more than 200 %. Again this can be explained by referring to Figure 1. For gas pipelines, the Reynolds number is higher than in the liquid line and the range is normally 5×10⁶<Re<1×10⁸. For this range, the friction factor curves in Figure 1 are apart from each other, so the friction factors are not close.
In summary, contrary to liquid pipelines the gas pipelines are very sensitive to wall roughness and using smooth pipe can reduce friction pressure drop considerably. This in turn lowers the OPEX. Therefore, regular pigging to clean the pipe surface is done to lower the roughness factor. The modern gas transmission companies will add a Fusion Bounded Epoxy (FBE) liner to gas pipelines because the pipe is sensitive to roughness.  This lowers OPEX for the long term. It should be noted that the smoother the pipe, the higher the CAPEX, so as always, detailed total cost analysis should be performed for engineering applications.
Due to the sensitivity of gas pipelines to roughness factor and other operation parameters, there are numerous gas flow equations (e.g. Weymouth, Panhandle A and B, AGA) to best fit certain design conditions [1].
To learn more about similar cases and how to minimize operational problems, we suggest attending our ME44 (Overview of Pumps and Compressors in Oil and Gas Facilities), ME46 (Compressor Systems – Mechanical Design and Specification), PL4 (Fundamental Pipeline Engineering), G40 (Process/Facility Fundamentals), G4 (Gas Conditioning and Processing), and PF4 (Oil Production and Processing Facilities) courses.

By: Dr. Mahmood Moshfeghian

Reference:

• Honeywell, Joe, “Friction Pressure Drop Calculation,” Campbell Tip of the Month, Feb 2007
• Campbell, J. M., “Gas Conditioning and Processing, Vol. 1, the Basic Principals, 8th Ed., Campbell Petroleum Series, Norman, Oklahoma, 2001
• Menon, E.S, Piping Calculations Manual, McGraw-Hill, New York, 2005