In this tip of the month (TOTM) we will present the compressor calculations of a case study. We will compare the rigorous method results with the values from the short cut methods. The rigorous method is based on an equation of state like the Soave-Redlich-Kwong (SRK) for calculating the required enthalpies and entropies. The enthalpies and entropies are used to determine the power requirement and the discharge temperatures. The results indicate that the accuracy of the shortcut method is sensitive to the value of heat capacity ratio, k.
Power Calculations
The theoretical power requirements are independent of compressor type; the actual power requirements vary with the compressor efficiency. In general the power is calculated by:
where mass flow rate and h is specific enthalpy.
From a calculation viewpoint alone, the power calculation is particularly sensitive to the specification of flow rate, inlet temperature and pressure, and outlet pressure. Gas composition is important but a small error here is less important providing it does not involve the erroneous exclusion of corrosive components. A compressor is going to operate under varying values of the variables affecting its performance. Thus the most difficult part of a compressor calculation is specification of a reasonable range for each variable and not the calculation itself. Reference [1] emphasizes that using a single value for each variable is not the correct way to evaluate a compression system.
Normally, the thermodynamic calculations are performed for an ideal (reversible process). The results of a reversible process are then adapted to the real world through the use of an efficiency. In the compression process there are three ideal processes that can be visualized: 1) an isothermal process, 2) an isentropic process and 3) a polytropic process. Any one of these processes can be used suitably as a basis for evaluating compression power requirements by either hand or computer calculation. The isothermal process, however, is seldom used as a basis because the normal industrial compression process is not even approximately carried out at constant temperature.
For an isentropic (reversible and adiabatic) process, equation 1 can be written as:
and based on the polytropic process:
The isentropic head is calculated by equation 3A:
Similarly, the polytropic head is calculated by equation 3B:
The actual discharge temperature based on the isentropic path is calculated by equation 4A.
The actual discharge temperature based on the polytropic is calculated by equation 4B.
where η and ηP are the isentropic (or adiabatic) and polytropic efficiency, respectively, P1 suction pressure, P2 discharge pressure, T1 and T2 arethe suction and discharge temperatures, respectively, q is gas volume flow rate at standard condition of PS and TS, Za average gas compressibility factor, k heat capacity ratio, R the gas constant, and n is the polytropic path exponent. Equations 1 and 2 are equally correct theoretically. The practical choice depends on the available data, although it is somewhat arbitrary. The power calculation should be made per stage of compression and then summed for all stages connected to a single driver. For general planning purposes the graphical solutions shown in reference [2] produce results comparable to these equations.
Equation of State (EOS)
The heart of any commercial process flow simulation software is an equation of state. Due to their simplicity and relative accuracy, normally a cubic EOS such as Soave Redlich-Kwong (SRK) [3] or Peng-Robinson [4] is used. These equations are used to calculate phase behavior, enthalpy, and entropy. With proper binary interaction coefficients, the process simulation results of these two equations are practically the same. Therefore, only the SRK was used in this work.
Step-by-Step Computer Solution
For known gas rate, pressure (P1), temperature (T1), and composition at the inlet condition and discharge pressure (P2), computation of compressor power requirement is based on an EOS using a computer and involves two steps:
- Determination of the ideal or isentropic (reversible and adiabatic) enthalpy change of the compression process. The ideal work requirement is obtained by multiplying mass rate by the isentropic enthalpy change.
- Adjustment of the ideal work requirement for compressor efficiency.
The step-by-step calculation based an EOS is outlined below.- Assume steady state, i.e. and the feed composition remain unchanged.
- Assume isentropic process, i.e. adiabatic and reversible
- Calculate enthalpy h1=f(P1, T1, and composition) and suction entropy s1=f(P1, T1, and composition) at the suction condition by EOS
- For the isentropic process
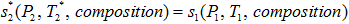 . Note the * represents ideal value.
. Note the * represents ideal value. - Calculate the ideal enthalpy (
 ) at outlet condition for known composition, P2 and
) at outlet condition for known composition, P2 and 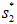 .
. - The ideal work is
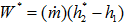
- The actual work is the ideal work divided by efficiency or
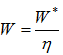
- The actual enthalpy at the outlet condition is calculated by
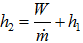
- The actual outlet temperature is calculated by EOS for known h2, P2, and composition.
The efficiency of the compressor, and hence, the compression process obviously depends on the method used to evaluate the work requirement. The isentropic efficiency is in the range of 0.70 to 0.90.
If the compressor head curve and efficiency curve are provided by the manufacturer, the head is determined from the actual gas volume rate at the inlet condition. Second, from the head, the actual work, discharge pressure and finally the discharge temperature are calculated.
Case Study
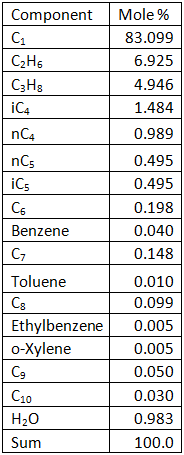
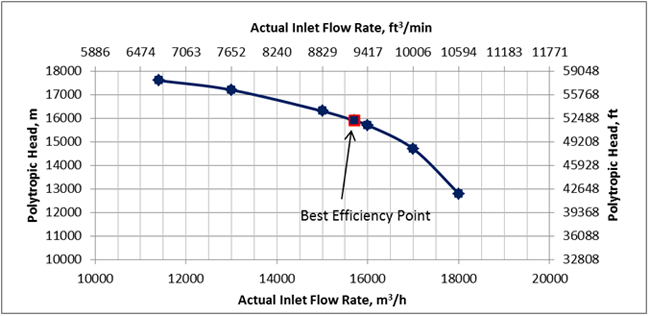
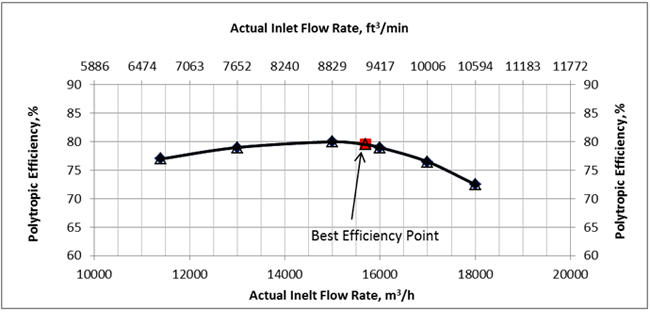
The gas mixture with the composition shown in Table1 at 105 °F (40.6 °C) and 115 Psia (793 kPa) is compressed using a single-stage centrifugal compressor with the polytropic head and efficiency curves shown in Figures 1 and 2 at a speed of 7992 rpm. The total feed gas volumetric flow rate was 101 MMSCFD (2.86×106 Sm3/d).
Table 1. Feed gas analysis
Figure 1. Compressor polytropic head and best efficiency point
Figure 2. Compressor polytropic efficiency
Results and Discussions
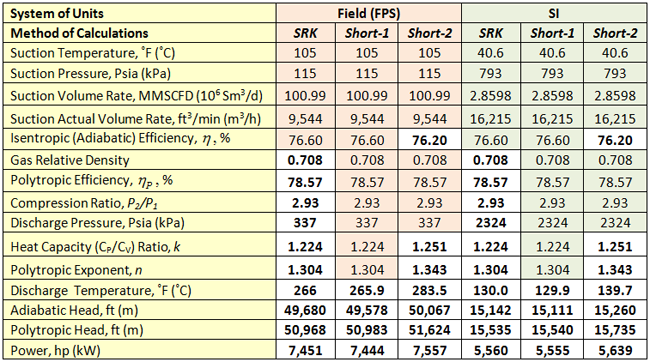
SRK (Rigorous Method): The feed composition, temperature, pressure, volumetric flow rate at standard condition along with the compressor polytropic head and efficiency curves data were entered into the ProMax software [5] to perform the rigorous calculations based on the SRK EOS. The program calculated polytropic and isentropic efficiencies, heads, compression ratio (discharge pressure), discharge temperature and power. For the actual gas flow rate at the inlet condition, the polytropic efficiency is close to the compressor best efficiency point (BEP). The program also calculated the gas relative density, heat capacity ratio (k), and polytropic exponent (n). These calculated results are presented in the SRK columns of Table 2 (bold numbers with white background).
Table 2. Summary of the rigorous and shortcut calculated results
The bold numbers with white background are the calculated values
Short-1 (Shortcut Method): In this method, we used equations 2 through 4 to calculate the polytropic and isentropic heads, the discharge temperature and power. We used the ProMax calculated polytropic and isentropic efficiencies, compression ratio (P2/P1), heat capacity ratio (k) and polytropic exponent (n) to calculate head, power, and the discharge temperature. The results are presented in the short-1 columns of Table 2. Note the short-1 results (discharge temperature, adiabatic and polytropic heads and power) are very close to the SRK values. The calculated actual discharge temperature by equation 4A (isentropic path: 265.3˚F=129.6˚C) was slightly lower than by equation 4B (polytropic path: 265.9 ˚F=129.9 ˚C).
Short-2 (Shortcut Method): Similar to short-1 method, we used equations 2 through 4 to calculate the polytropic and isentropic heads, the actual discharge temperature and power. We used only the ProMax calculated values of polytropic efficiency (nP), compression ratio (P2/P1), and relative density (y). The heat capacity ratio (k) was estimated by equation 5:
The polytropic exponent (n) was estimated by equation 6.
The isentropic (adiabatic) efficiency () was estimated by equation 7.
The results for this method are presented in the short-2 columns of Table 2. The calculated discharge temperature by equation 4A (isentropic path) was exactly the same as by equation 4B (polytropic). Note the short-2 results (discharge temperature, adiabatic and polytropic heads and power) are deviated from the SRK values.
The results in Table 2 indicate that an increase of 2.2% in k (from 1.224 to 1.251) results in power increase of 1.42%. The polytropic exponent (n) increased by 3% and isentropic efficiency (![]() ) decreased by 0.5 %. The difference in the actual discharge temperatures of the SRK and short-2 values is 17.5 ˚F (9.7˚C).
) decreased by 0.5 %. The difference in the actual discharge temperatures of the SRK and short-2 values is 17.5 ˚F (9.7˚C).
With the exception of actual discharge temperature, these differences between the SRK and short-2 methods results for facilities calculations and planning purposes are negligible. Note that the accuracy of the shortcut method is dependent on the values of k and n. In Short-1 method in which we used the k and n values from the SRK method the results were identical to those of SRK method.
To learn more about similar cases and how to minimize operational problems, we suggest attending the John M. Campbell courses; G4 (Gas Conditioning and Processing), and G5 (Gas Conditioning and Processing-Special).
John M. Campbell Consulting (JMCC) offers consulting expertise on this subject and many others. For more information about the services JMCC provides, visit our website at www.jmcampbellconsulting.
By Dr. Mahmood Moshfeghian
Reference:
- Maddox, R. N. and L. L. Lilly, “Gas conditioning and processing, Volume 3: Advanced Techniques and Applications,” John M. Campbell and Company, 2nd Ed., Norman, Oklahoma, USA, 1990.
- Campbell, J. M., “Gas Conditioning and Processing, Vol. 2, the Equipment Modules, 8th Ed., Campbell Petroleum Series, Norman, Oklahoma, 2001
- Soave, G., Chem. Eng. Sci., Vol. 27, pp. 1197-1203, 1972.
- Peng, D. Y., and Robinson, D. B., Ind. Eng. Chem. Fundam., Vol. 15, p. 59, 1976.
- ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2011.

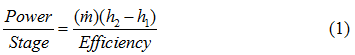
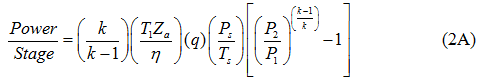
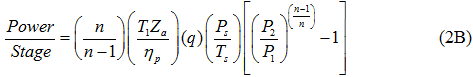
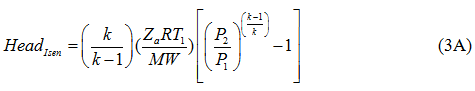
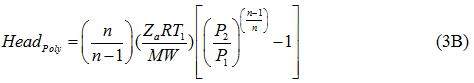
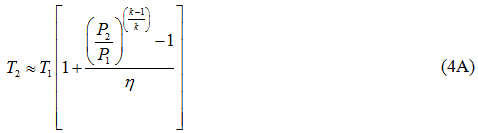

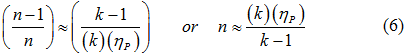
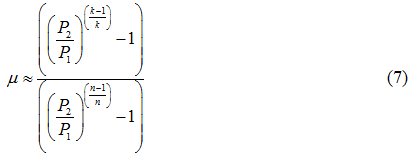
Compressor
Could you please advise whether the values of ‘k’ used in the two methods were based on the Cv=Cp-R (Ideal Gas) relationship or ‘real’ values of Cv calculated directly from the EoS? This can have a significant impact on the results, e.g. incorporating ‘real’ values of ‘k’ (from HYSYS) into the API equations for relief valve sizing can over-estimate the capacity of a given orifice.
Joe,
k=Cp/Cv is based on the ideal gas heat capacity ratio.
Dear Dr. Mahmood,
Thanks for this article.
I would just like to know two things.
1. What is the basis of eqn 5? Did you make a linear best fit in excel in between the dependent variable k and independent variable y and arrived at the eqn.?
2. When heat capacity ratio (k) is meant, is it Cp/Cv or Cp/(Cp-R) (i.e., an ideal gas heat capacity ratio)?
I would be greatful, if you could provide me the answers.
Thanks,
Rahul Mukherjee
Rahul.Mukherjee@veco.com
Rahul,
1. Equation 5 is purely empirical, based on typical natural gases that contain no substantial quantities of non-hydrocarbons and whose relative density does not exceed one.
2. k=Cp/Cv is the ideal gas heat capacity ratio.
Dear Dr. Mahmood,
As per your response above, k is the ideal specific heat ratio based on Cv=Cp-R as the article demonstrates simple hand calcs without a process simulator for EOS calcs. If you were carrying out calculations on a non ideal gas (e.g. Z = 0.8), and could obtain actual specific heat ratio from a process simulator, would this be the correct approach (or would you still have to use ideal specific heat ratio)?
Dr Mahmood
I just want to calculate efficiency and head for air compressor having the several points of suction pressure vs flowrate in m3/h. Please help..
Thank you
Please Sir,how do i find d expression for entropy for a soave-redlich kwong equation of state ?
Dear Mahmood:
One important question in my mind. How can one calculate discharge temperature in oil injected compressor in Hysys or any other process software?
Hello Dr. Moshfeghian,
I have written a procedure for measurement flow of a CNG compressor in refueling station. Is it possible for me to send the procedure for you to check if that is correct or not?
Thank you
Before you paint ceiling and walls, follow the 9 feet
guideline. Virtually all children go through a period in which they appear to be knock-kneed when strolling.
Include sophistication to your place with
a couple of accessories to the door is a smart and easy way.
Interesting Material. My question is about the change in calculations when applied to a stream of Acid Gas containing CO2/H2S with trace of Hydrocarbons?
How about the case with Flue gas compression?
ı want to choose a compressor for a Project
ı have tow things
for EX:
Room Name: WELDING ROOM
Room Area: 79 m2
Plumbing: Service sink (hot and cold water), (2) compressed air drops 0-1034kPa each, 345 kPa minimum to down flow station, 620-1034 kPa to plasma cutter.
and there is another things but like that
can help me Dr for knowing the Flow.Velocity for this compressor
thx
Thank you very much!
Hi Doc,thanks for the nice educating post.My question is;Are equations 2A,2B,3A,3B,4A and 4B applicable to real gases?
Dr. Thanks for the nice writeup. How do we estimate the k value and gamma value when we inject known volumetric flows of wash oil or water to cracked gas compressor stages to mitigate fouling due to polymerization?. This has been the challenge. Please help.
Thanks
Venkat
hello
i wonder if anyone can help me , i need to find the adiabatic efficiency of a compressor we are prototyping. i am by no means a mathematician and all these equations are really confusing me. if someone could explain to me what all the letters stood for it would be a great help
many thanks
Adamson:
Method 1:
1. Knowing gas molecular weight (MW) estimate, gas relative density or Specific Gravity by SG=MW/29
2. Plug in SG (the Greek letter gamma) into equation 5 to estimate k (ratio of specific heats at the ideal gas conditions).
3. Knowing compressor polytropic efficiency provided by the vendor calculate n by equation 6 (the 2nd one on the right hand side. n= polytropic exponent.
4. Use equation 7 to estimate the adiabatic efficiency (the Greek letter, mu). P1 and P2 are the suction and discharge pressures, respectively.
Note: All T’s and P’s are absolute value
If the polytropic efficiency is not available, one can use use the following procedure for a working compressor:
Method 2:
1. Measure suction pressure (P1), suction temperature (T1), and discharge pressure (P2), discharge temperature (T2).
2. Calculate compression ratio = R = P2/P1
3. Raise compression ratio to power of (k-1)/k or CR=(P2/P1)^[(k-1)/k]
4. Estimate adiabatic efficiency = T1(CR-1)/(T2-T1). This rearrangement of equation 4A.
Note: All T’s and P’s are absolute value
Method 3:
1. Measure suction pressure (P1), suction temperature (T1), and discharge pressure (P2), discharge temperature (T2).
2. Use a Pressure-Enthalpy-diagram for your gas or a computer program to calculate: Suction enthalpy (H1) at P1 and T1, discharge enthalpy H2 at P2 and T2, discharge isentropic enthalpy H2ise.
3. Estimate adiabatic (isentropic) efficiency by:
Adiabatic efficiency = (H2ise – H1)/(H2-H1)
The detail of this topic is covered in our G4 (Gas Processing and Conditioning) course.
I hope this helps.
This keeps players glued to their monitors
to make sure they don’t miss a thing. So decide if you are irritated, or happy with the color and
sound of the poker room to sign in. Those cards drop down and become part of the hand on the
second line. Of course there is some sumptuous finger food
to take care of your appetite.
Dear Sir,
Can you please tell me any relation between Steam Enthalpy and RPM of a Steam Turbine. How they affect each other?
DreamProxies.com – least expensive top-notch private proxies with 50% low cost! Professional quality, Unrestricted proxies, Very speed along with Cheapest price ranges – simply $0.25 for every proxy! Finest individual proxies just from DreamProxies.com
Merely wanna tell that this is very useful, Thanks for taking your time to write this.
I gotta bookmark this site it seems very helpful very useful
Hello sir,
Can the polytropic efficiency of compression be greater than unity,when n is less than k (i.e 1<n<k).
since using the polytropic efficience [(k-1)/k]/[(n-1)/n] will be greater than 1.
DreamProxies.com — least expensive top-notch private proxies with 50% low cost! Elite quality, Limitless proxies, Very speed and Cheapest prices : only $0.25 for each proxy! Best non-public proxies just on DreamProxies.com
Guys who of you play Pokemon GO? Incredible game, finally Lickitung has been caught
using pokebusterbot. With this bot you can catch pokemons on autopilot!
how should calculate polytropic efficiency of single stage compressor with suction and discharge pressure and temperature and gas composition
https://www.degruyter.com/view/j/tjj.ahead-of-print/tjj-2016-0029/tjj-2016-0029.xml
For low pressures and relatively high temperatures, you can also use the ideal gas law instead of cubic equations of state ..
Where is the use of compressibility factor while calculating discharge temp T2 in adiabatic compression for non-ideal gas?
Dr. Mahmood,
I had put up a query about how to use compressibility factor for calculating adiabatic discharge temperature? Whenever z defers significantly from 1 for example for ethylene at pressure of 100 bar, how to use Z for calculating adiabatic discharge temperature. Request help.
What is the formula to calculate compressor number? if there is given compression rartio or somethimg like that.
I am looking for a vendor that publishes isentropic compressor efficiencies as a sales point…akin to COP for a refrigerator. Can you provide vendor that does such? Nice web page, thanks.
GE and Burckhardt Compression are likely vendors to define isentropic efficiency.
These “Tip of the month” pages are really insightful.
Would these equation work for an oil injected twin rotary screw compressor?
help solve this:
Calculate the power required to overcome the internal losses in an electrically driven turbo compressor operating under the following conditions: Suction volume : 1140 m^2/min Temperature : 27 ˚C Pressure : 0.85bar (abs) Deliver temperature : 104 ˚C Pressure : 6.5bar (abs) Motor load : 5850 w
Work done = n/( n-1)(P_2 V_2-P_1 V_1)
Interesting forum